At its core, KOE will be as useful as our estimate of converting a field goal \(\hat{p}_{FG}\) resembles \(p_{FG}\). In order to do this as well as possible, the information fed into the model must help it distinguish how hard each attempt actually was.
What determines the difficulty of a kick? The answer is surely as complex as our information allows it to be, but we will try to build a model as simple as possible that best answers this question. A secondary objective with the features is to make our model depend as less as possible on variables that could be hard to obtain on any given moment during a game.
The following variables were tested for their contributions:
- Kick Distance
- Score Differential
- Dome
- Game Seconds Remaining
- Maximum Temperature1
- Minimum Temperature2
- Precipitation3
- Local
- Half Seconds Remaining
- Win Probability
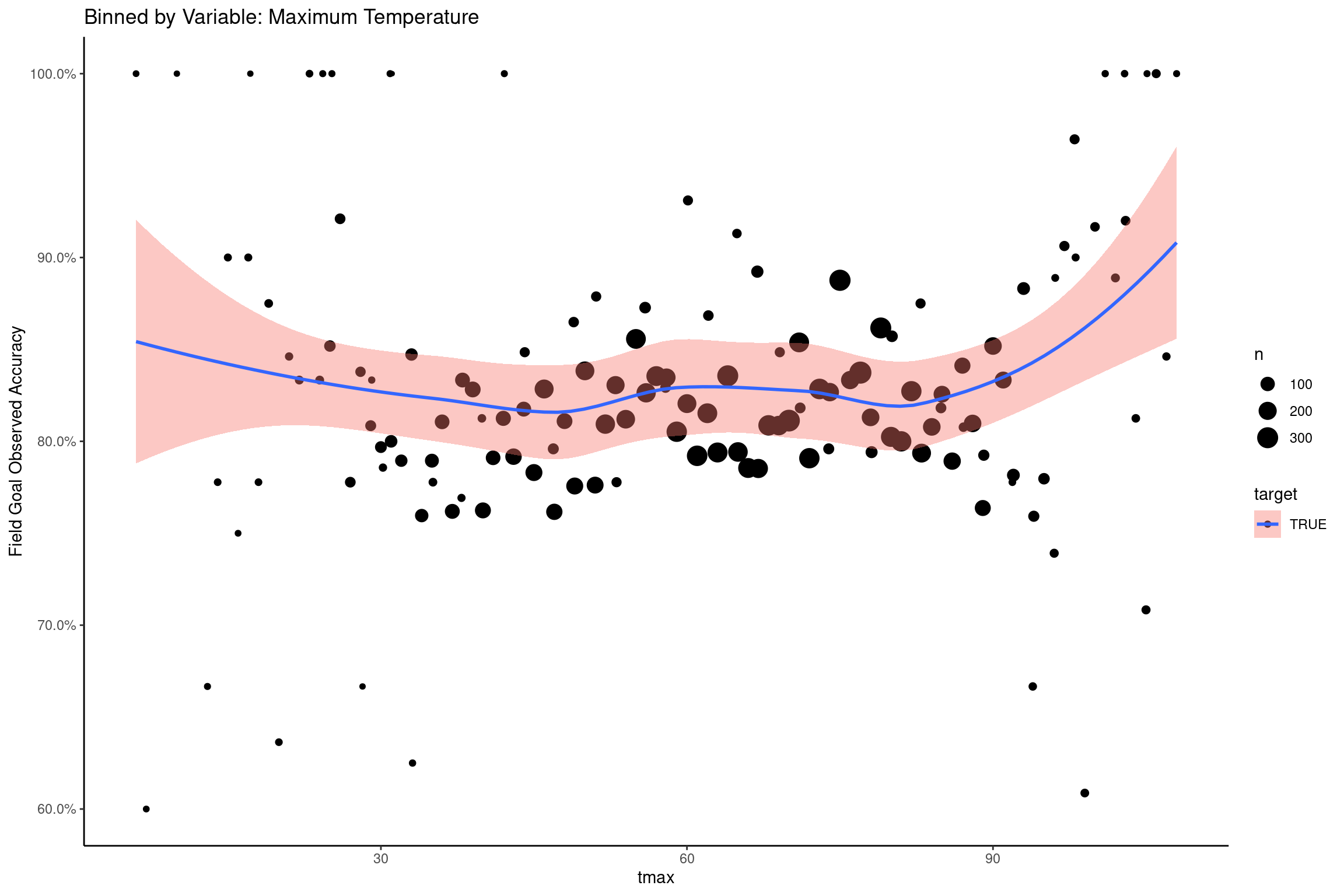
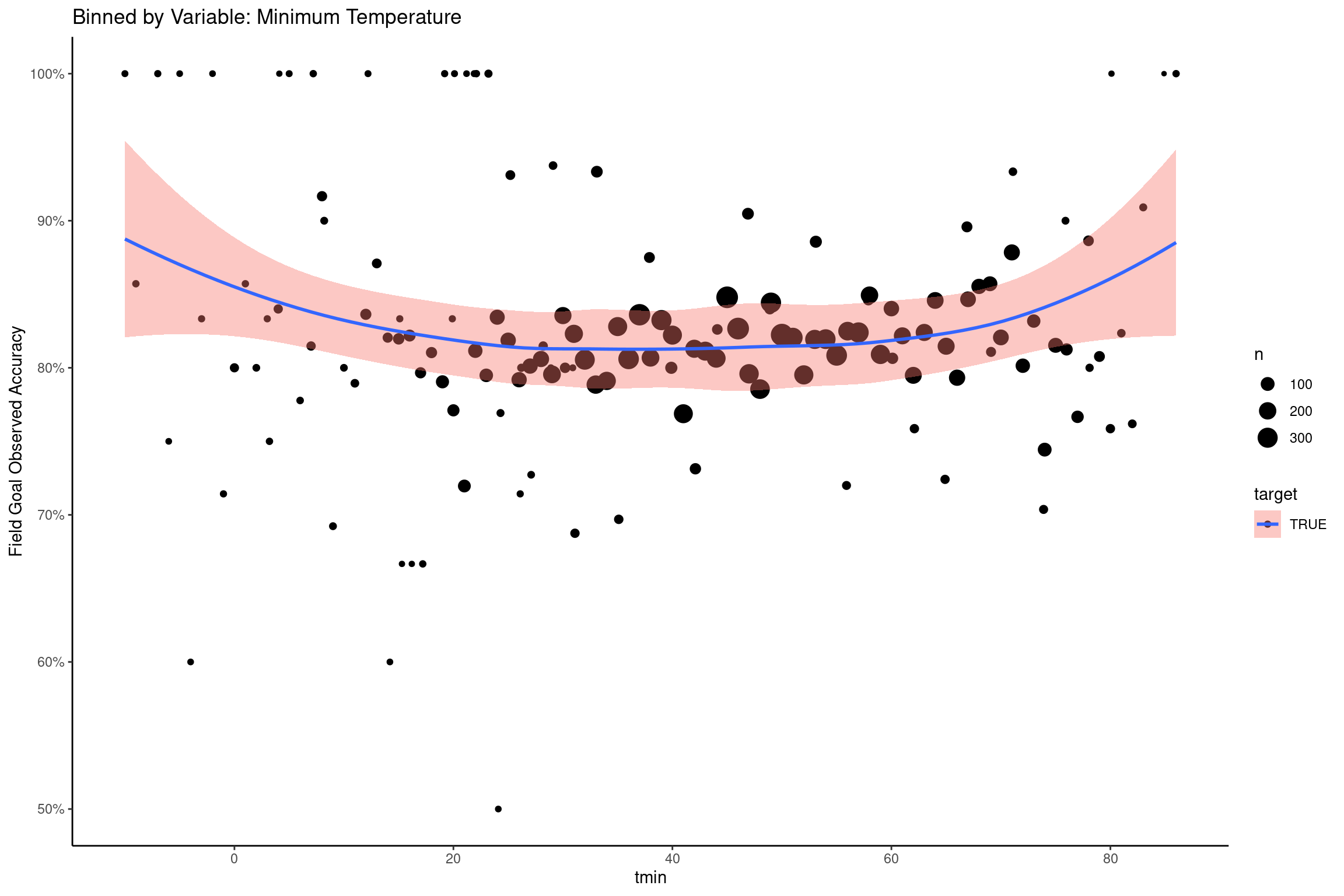
Maximum Temperature and minimum Temperature
Field Goals attempted on domes were excluded from the following figures. There is some visible tendency of field goals to become less accurate as the temperature is lower, and this is perhaps more visible in the case of maximum temperature.
Score Differential
Did not appear to be useful, but was still tested when modelling.
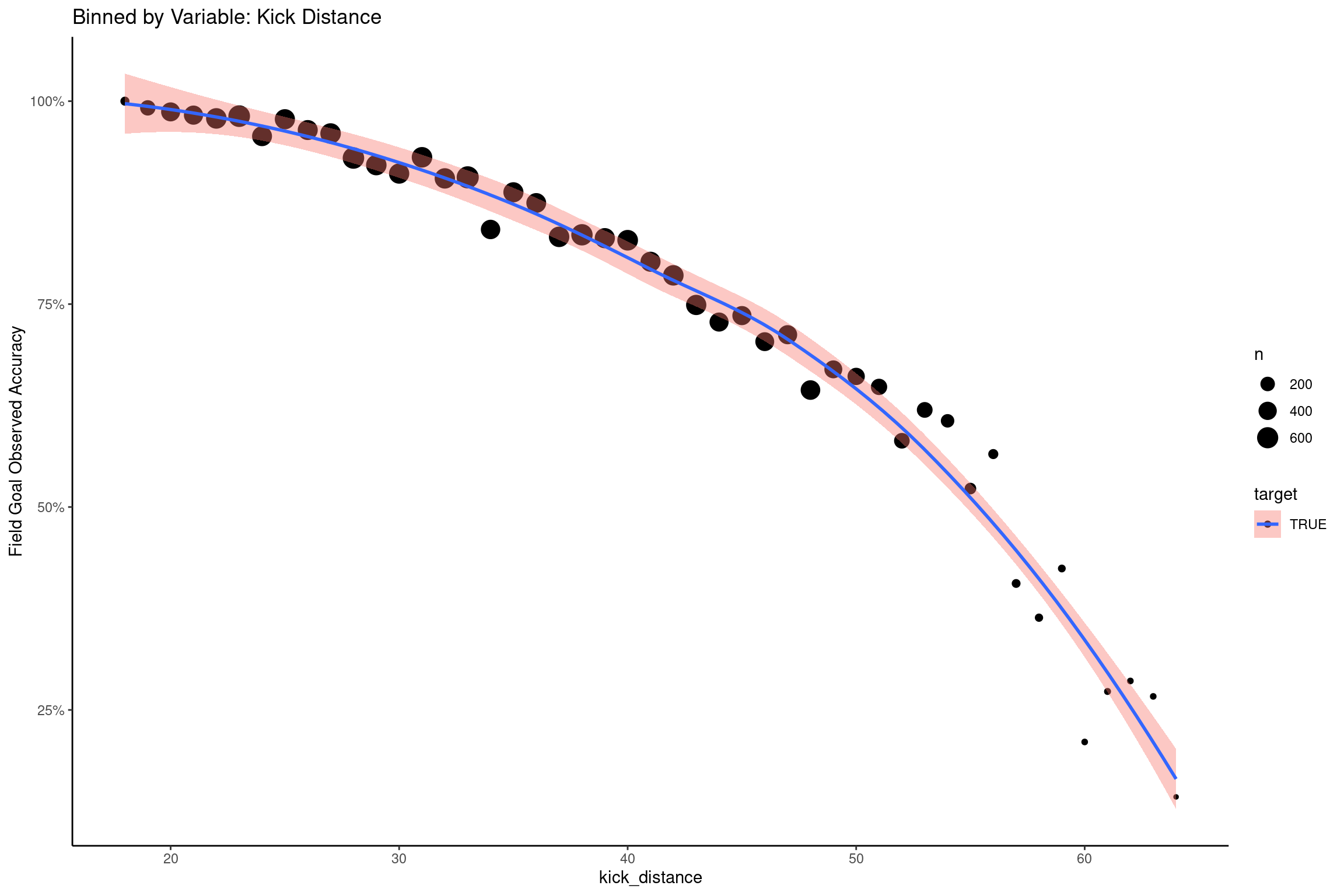
Kick Distance
Kick distance is perhaps already a pretty good predictor by itself. It appears we could predict using only the frequency counts displayed in the plot and we would not be so far off.
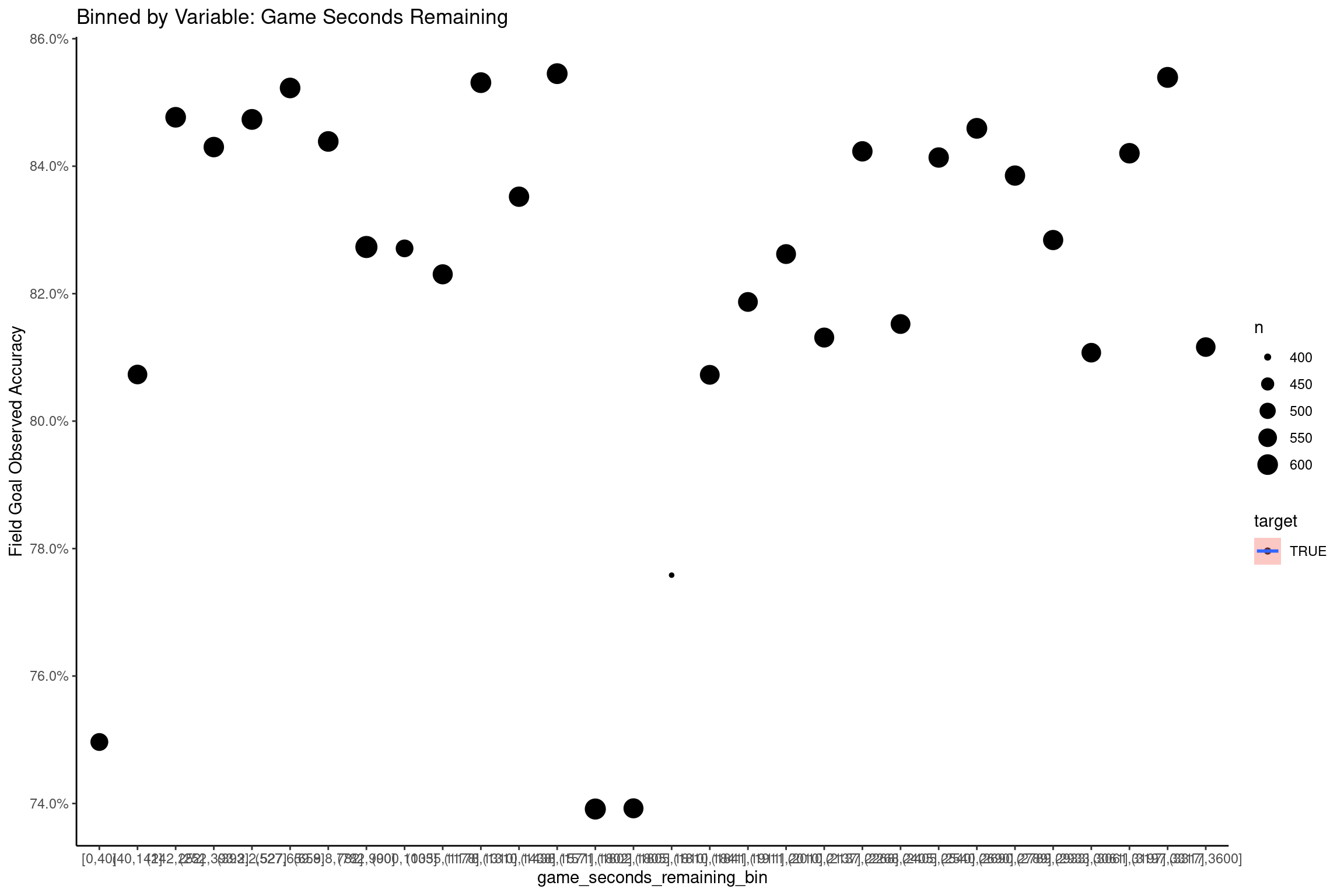
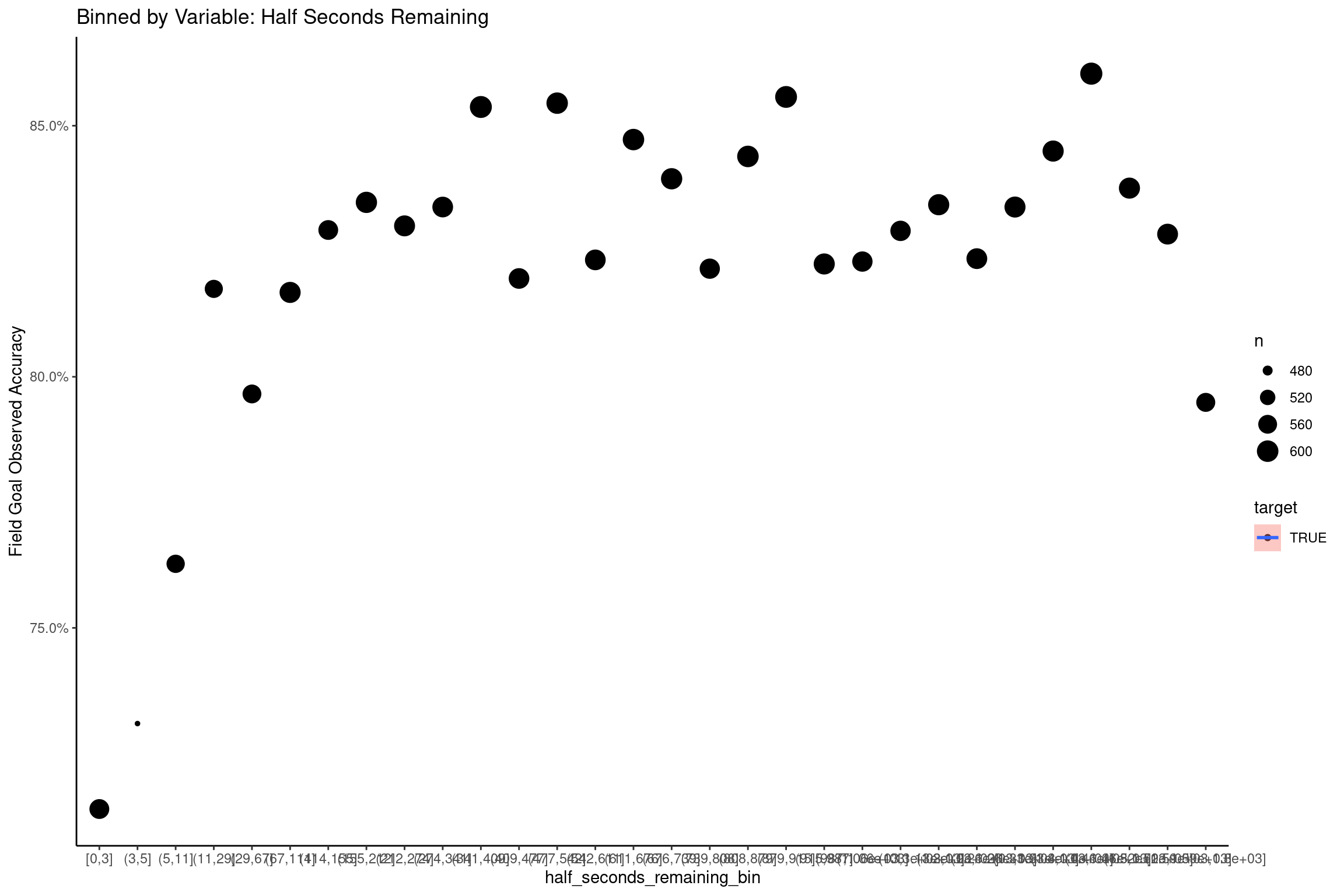
Game Seconds Remaining and Half Seconds Remaining
Field goal accuracy does not appear to be affected by the time remaining on the clock, except for kicks attempted less than 1 minute before the half ends. This same pattern appears on end of half and end of game situations, and suggests coaches are often forced to take their shot at points outside of what would be a reasonable distance for their kickers.
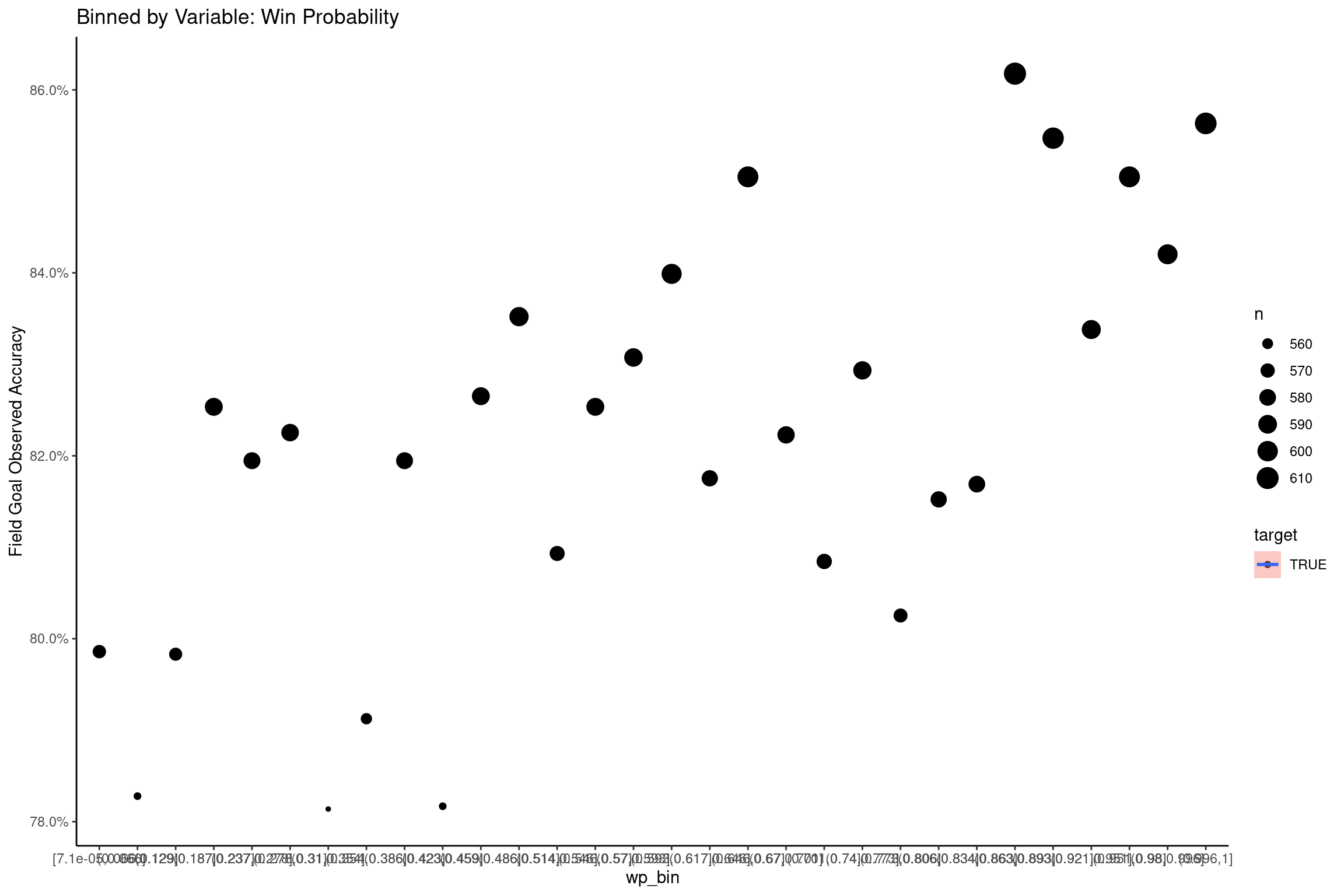
Win Probability
Win probability from the nflfastR model was also tested as a feature. The interpretation of these results are perhaps intuitive, but still surprising. As games get out of reach, kickers become less accurate, and the opposite happens when the kicking team dominates. This could be a proxy for the psychological aspect of kicking that is often mentioned when disscusing the subject.
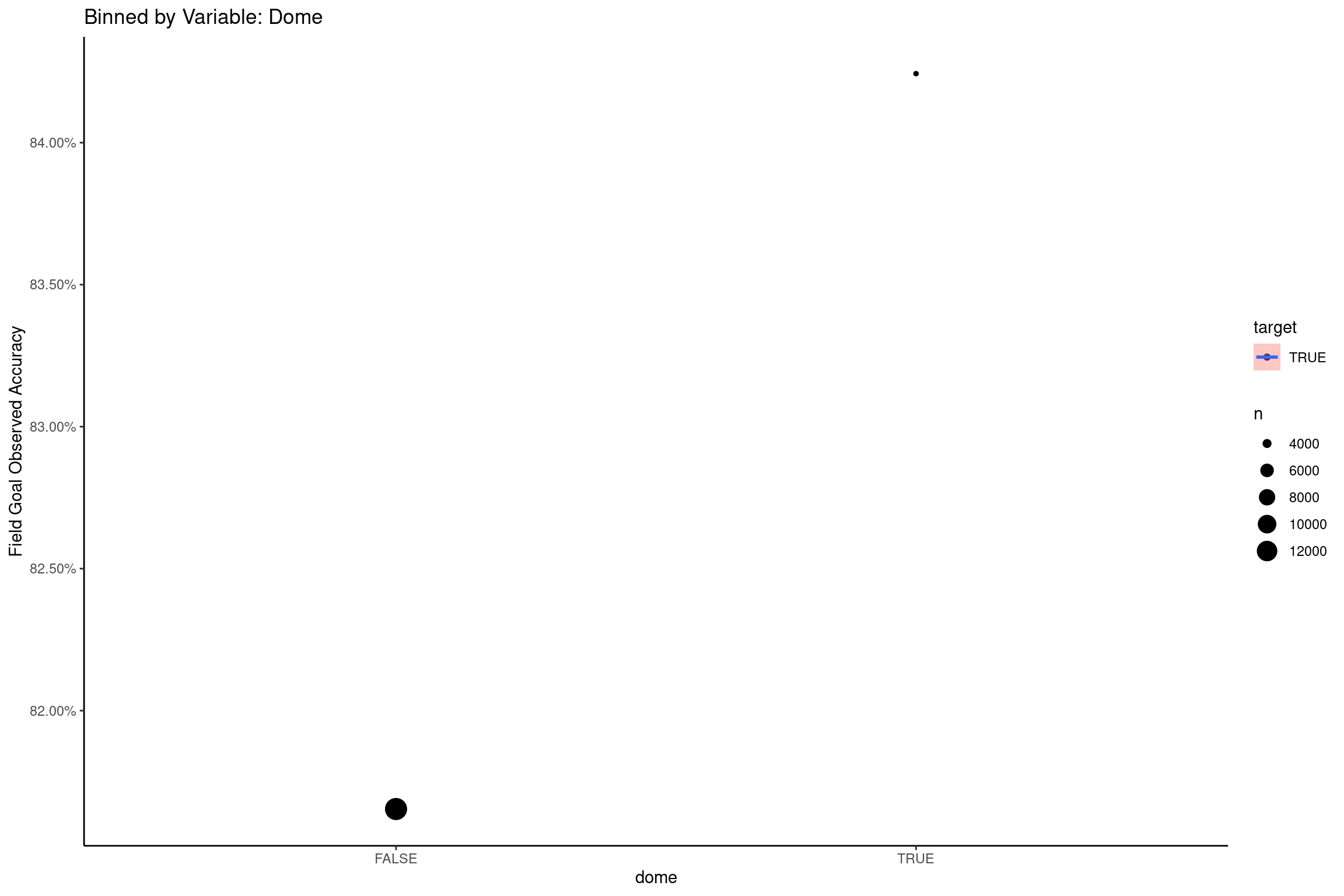
Dome and Stadium
The dome variable takes a 0 or 1 depending on if the stadium is closed or open. The definition may not always be as binary, but this model has the assumption that a stadium is either a dome or not, in the sense that it has controlled weather. This is considered a safe assumption because even while new stadiums can be opened or closed, the home team is not expected to opt for harsher weather.
There are a lot less attempts to measure on domes, but there is a visible change in the probability when attempting a FG from one. Its almost 3% more likely to convert when attempting a kick from a “closed” stadium.

We define the expert feature clutch which is binary variable that indicates if the kick was attempted on the 4th quarter with less than 5 minutes to go. Not surprinsingly, this impacts significantly in making a field goal more difficult.
plot_var_cat("clutch","Clutch")## `summarise()` regrouping output by 'var_1' (override with `.groups` argument)## `geom_smooth()` using method = 'loess' and formula 'y ~ x'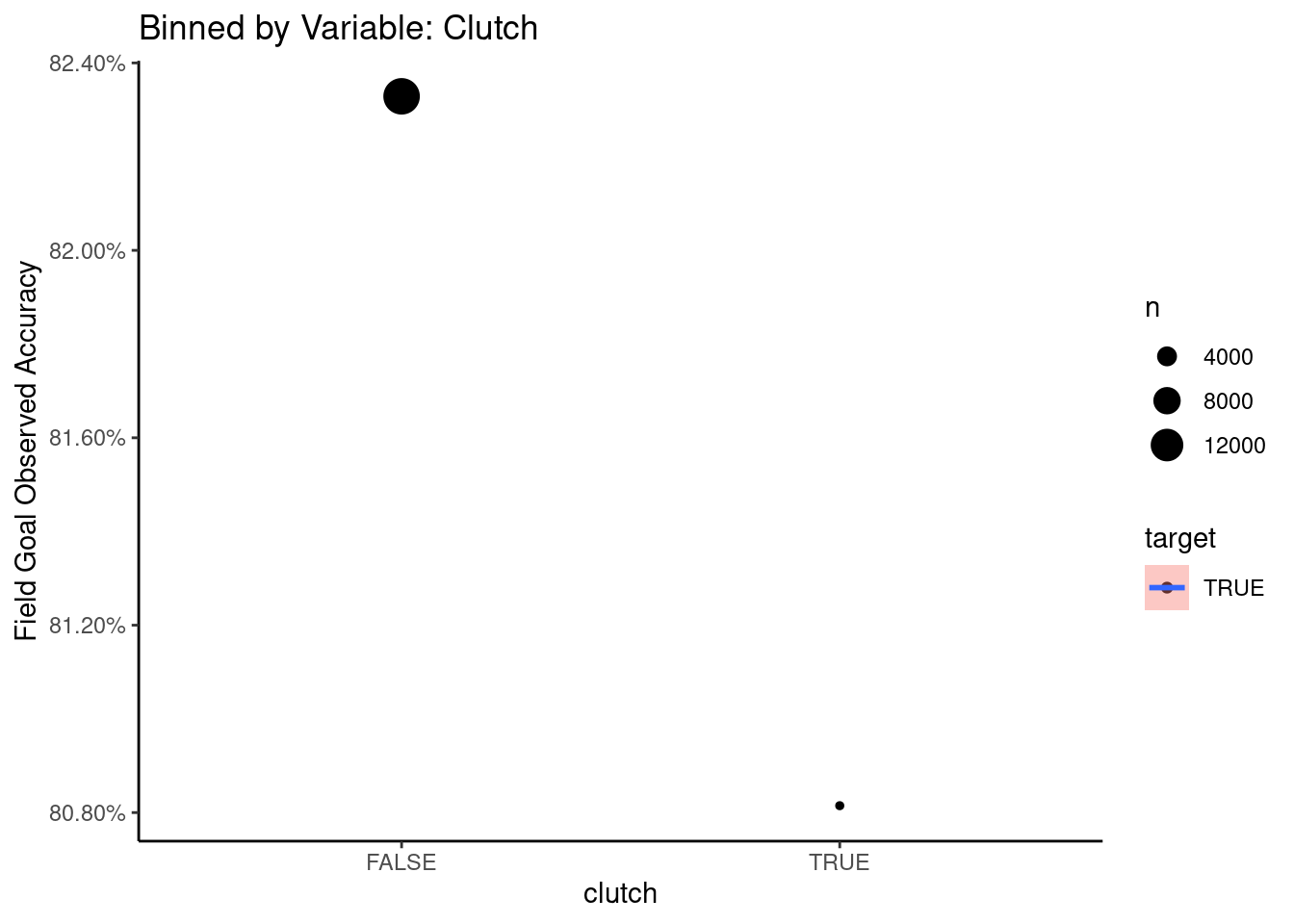
Lead Change
A second expert feature is defined Lead Change which is binary variable that indicates if the kick was attempted when the score differential was between -3 and 3. The logic behind this is that IF a kicker is getting nervous about taking the lead, or getting *his one lead out of reach, it should show here.
There appears to be an influence, however it would be interesting to see how diffent this would look excluding clutch plays. Both were tested in the model as separate features.
plot_var_cat("lead_change","Lead Change")## `summarise()` regrouping output by 'var_1' (override with `.groups` argument)## `geom_smooth()` using method = 'loess' and formula 'y ~ x'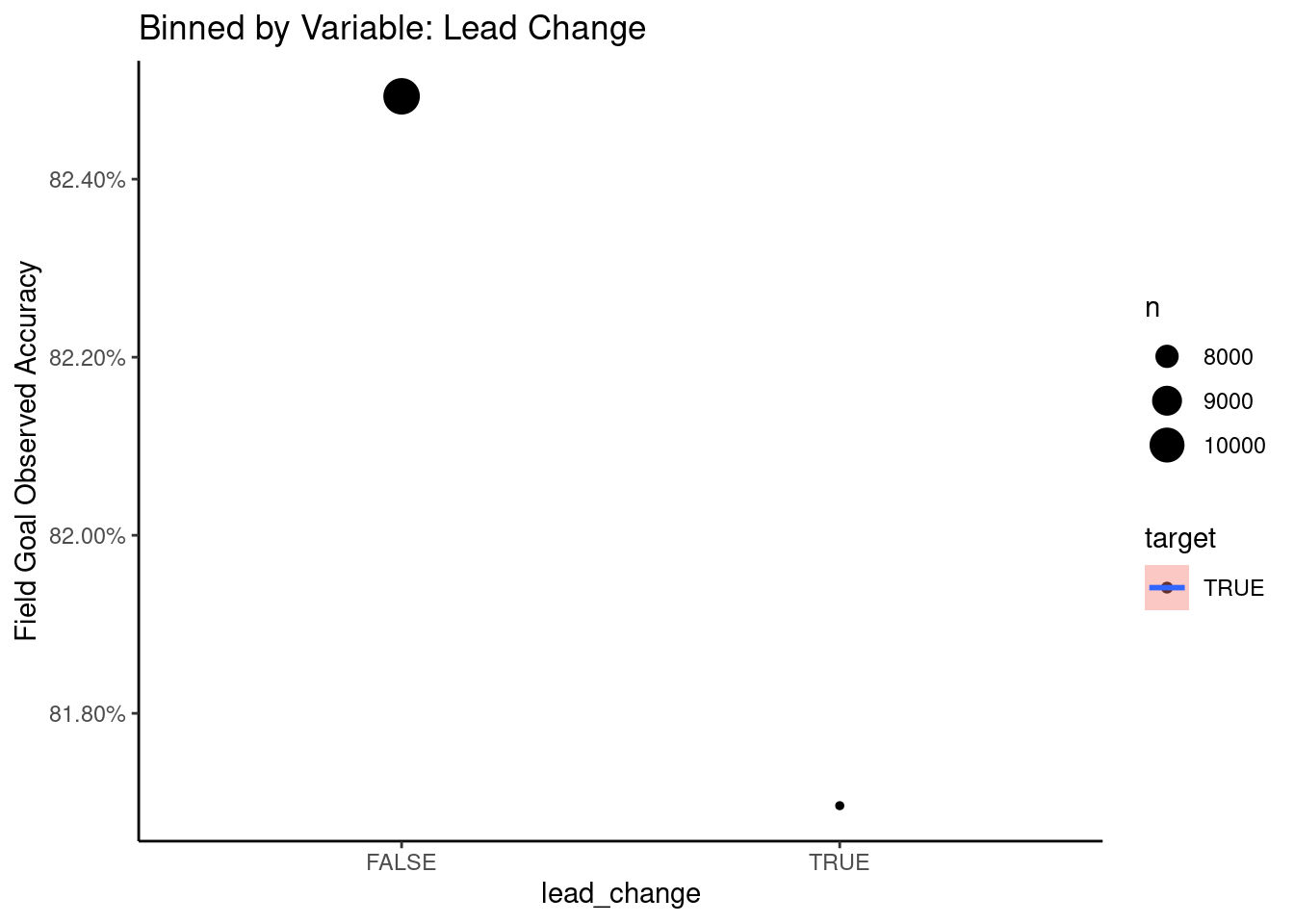
Closest measuring station to stadium from https://figshare.com/articles/dataset/Compiled_daily_temperature_and_precipitation_data_for_the_U_S_cities/7890488↩︎
Closest measuring station to stadium from https://figshare.com/articles/dataset/Compiled_daily_temperature_and_precipitation_data_for_the_U_S_cities/7890488↩︎
Closest measuring station to stadium from https://figshare.com/articles/dataset/Compiled_daily_temperature_and_precipitation_data_for_the_U_S_cities/7890488↩︎