The best model for our purposes has to be as simple and accurate as possible. If the methodology suggested is free of assumptions that become invalid with changes in the distribution, there is no reason why it could not reproduce comparable results in different leagues and countries.
A holdout set of all kicks attempted since 2019 was taken to prevent myself from over-fitting the problem. Only plays when a field goal was actually attempted are included, so only three possible outcomes were considered:
- Field Goal Made
- Field Goal Missed
- Field Goal Blocked
Various models and preprocessesing steps were tested, including:
- Logistic Regression
- Stepwise Regression
- Random Forest
- XGBoost
- Multi-Layer Perceptron
Results
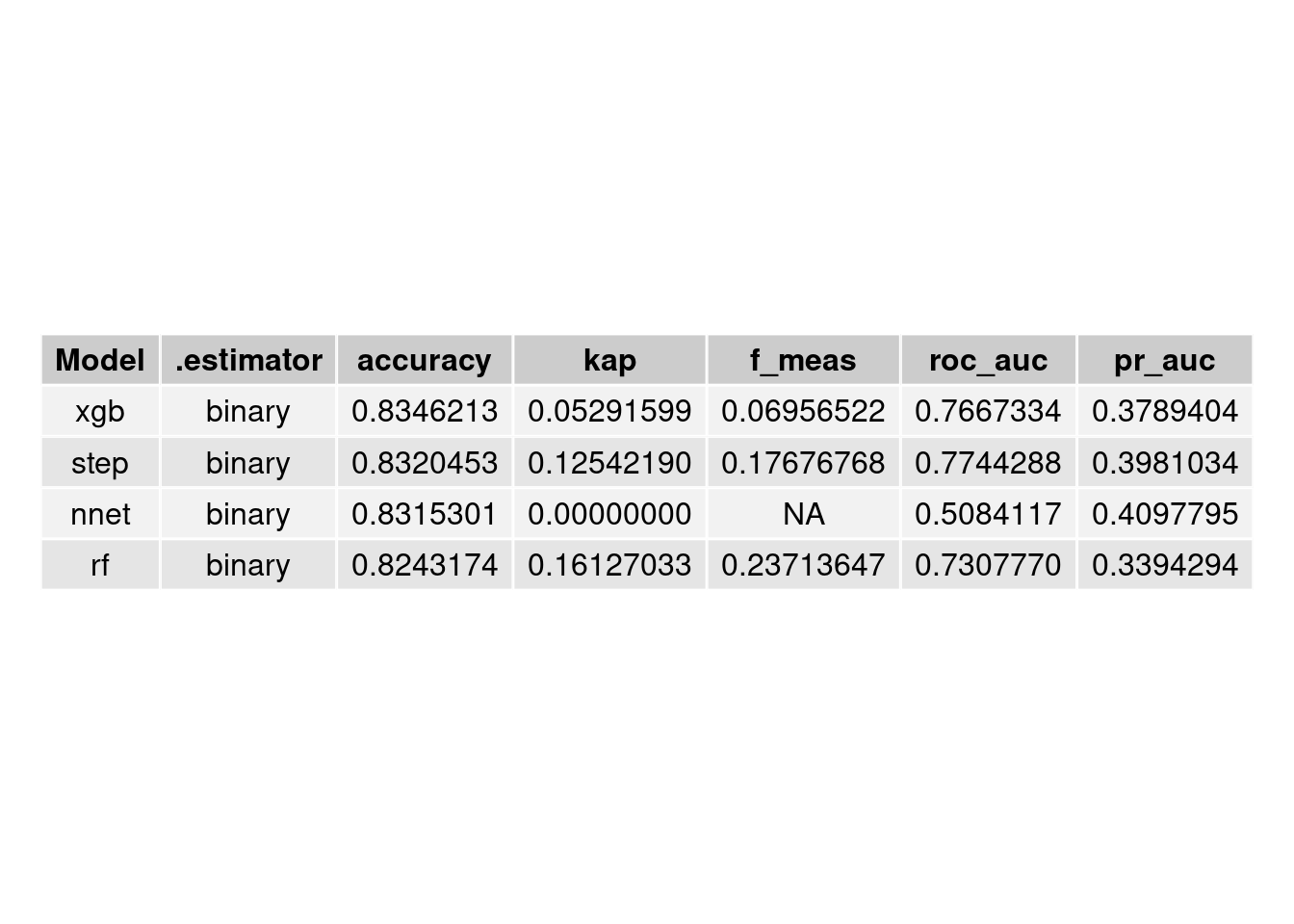
The model chosen was a “trained Stepwise Regression”, however this is nothing else than a logistic regression that was chosen for its lower AIC by an algorithm. Every attempt to improve the AUC and KS resulted in at best a comparable model to our trusty Logistic Regression. Model tuning was attempted using XGBoost, which resulted in a slightly better AUC, but that in the opinion of this author is a much worse and less elegant solution to our problem. Maybe a more accurate model can still be built, but at the moment no approach that remains blind to the kicker behind the attempt was found.
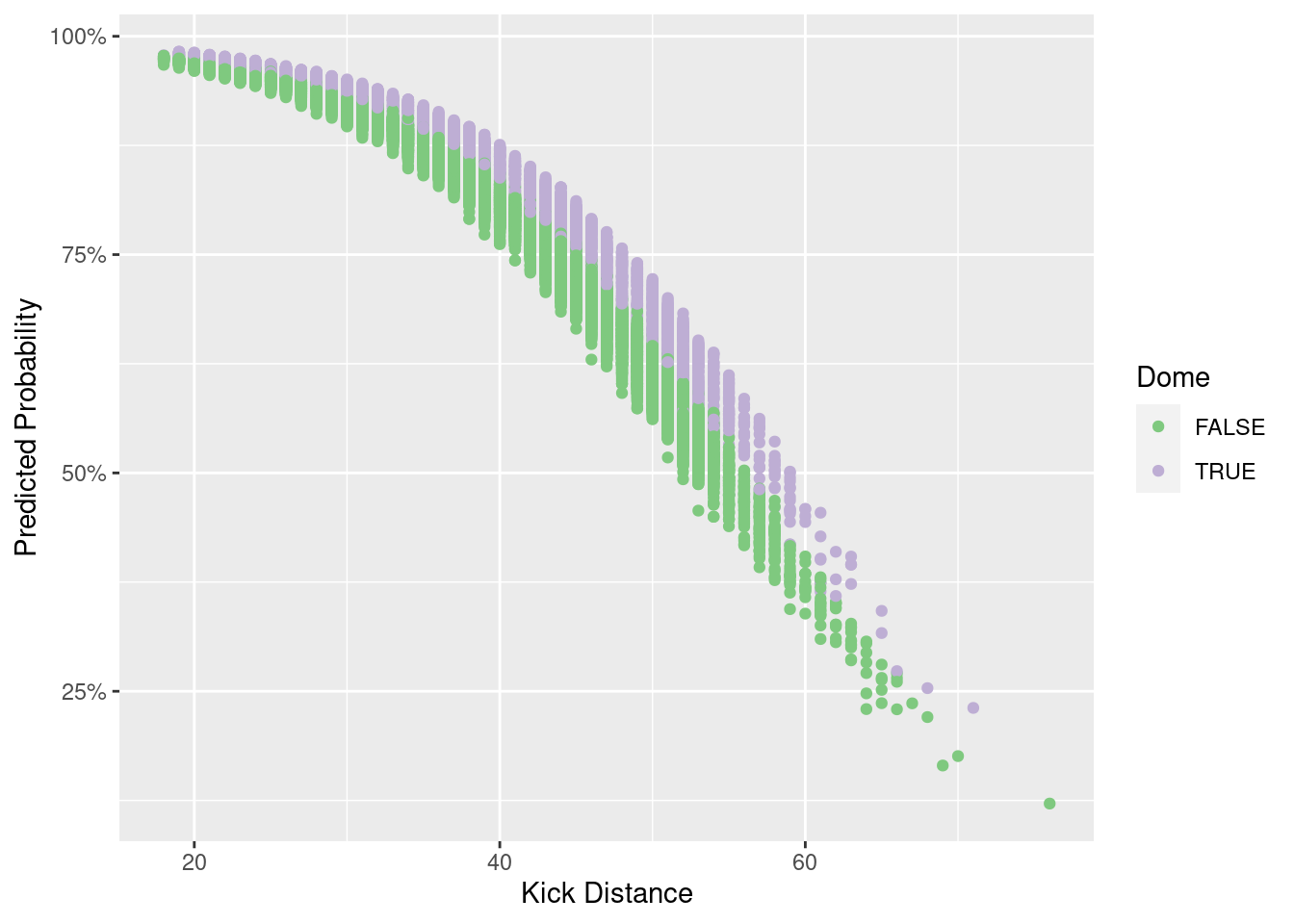
Inspecting the final model to be used from now on we can see it is only using three of our features:
- Kick Distance
- Dome
- Maximum temperature
Its important to remember that while our coefficients are interpretable, they have an effect on log-odds, and not FG probability directly.
##
## Call:
## NULL
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.7959 0.2681 0.4263 0.6660 1.7155
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 5.084939 0.142984 35.563 < 2e-16 ***
## kick_distance -0.099830 0.002776 -35.958 < 2e-16 ***
## domeTRUE 0.332055 0.062625 5.302 1.14e-07 ***
## tmax 0.005505 0.001384 3.978 6.95e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 12723 on 13526 degrees of freedom
## Residual deviance: 11099 on 13523 degrees of freedom
## AIC: 11107
##
## Number of Fisher Scoring iterations: 5Our model seems to be consistent thorugh its different ranges of predictions, with similar observed probabilities than predicted.
## `summarise()` ungrouping output (override with `.groups` argument)## `geom_smooth()` using formula 'y ~ x'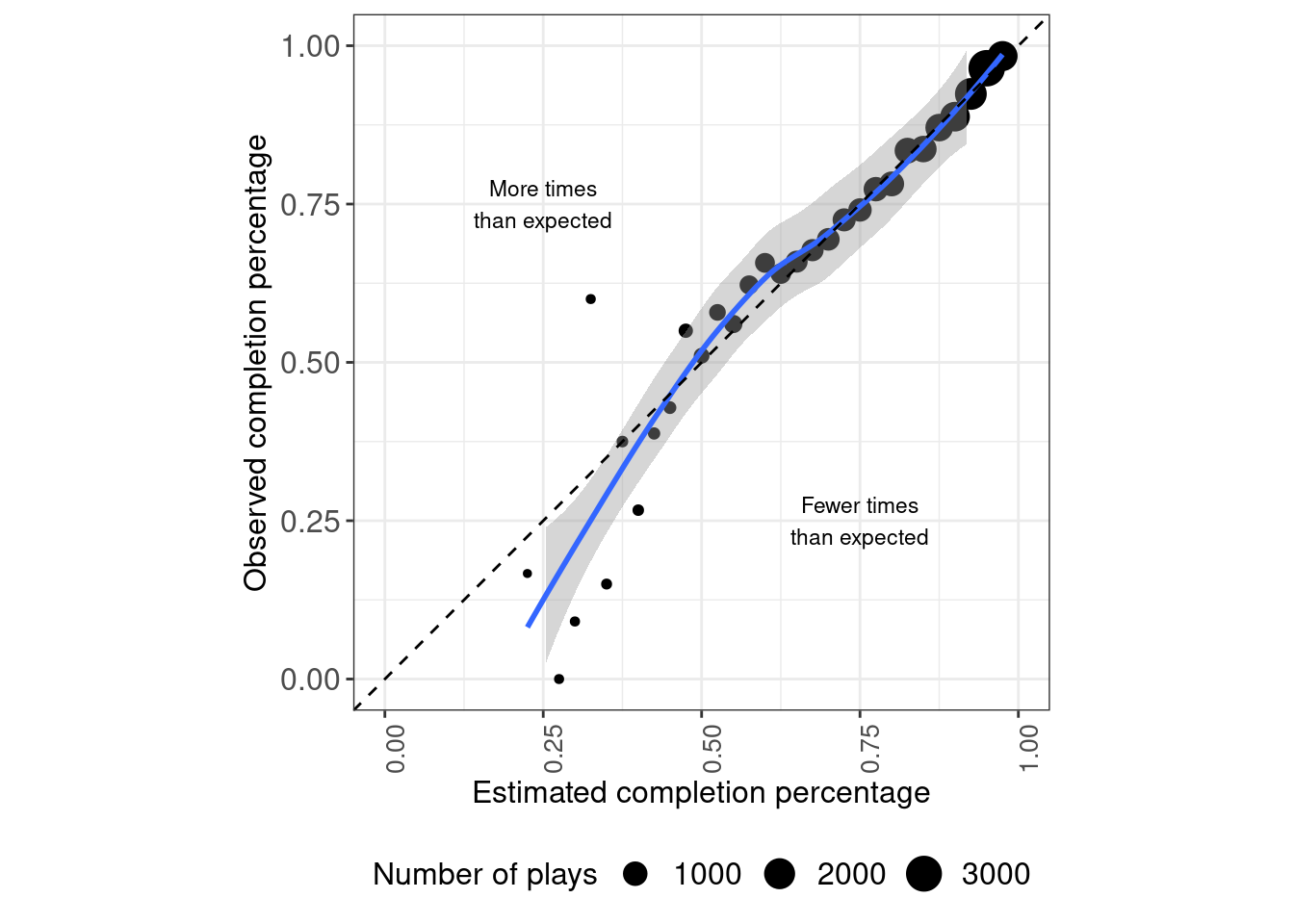
A closer look at our model against our variable, reveals how it works underneath, being determined mostly by kick distance, with a minor adjustment when the game is played on a dome. Also, very low temperatures also appear to have a strong effect, and it seems to amplify as the distance is longer.